[Swedky]

Hola, estoy trabajando en mi include PHY y estoy bastante avanzado en algunas cosas, pero lo que quiero saber es una fуrmula para conocer la distancia que recorrerб el objeto sabiendo la velocidad inicial, el бngulo de inclinaciуn inicial y la gravedad (creo que con esos valores se podrнa).

Por ejemplo: la velocidad inicial es de 10m/seg cuadrado, el бngulo de la inclinaciуn inicial es de 80° y la aceleraciуn/desaceleraciуn por gravedad es de 9.81m/seg cuadrado, їcuбnta distancia recorrerб?

Si podrнa estar expresado cуmo se lo harнa en PAWN, se lo agradecerнa.
Un saludo.

[JeffreyG]

Por lo que leн tenes que saber el tiempo de vuelo, y sustituirlo en esta ecuaciуn, esto te va a dar el alcance, osea la distancia que recorrerб el objeto:

x=vx⋅t=v0⋅cos(α)⋅t

El tiempo de vuelo se calcula igualando a 0 la componente vertical de la posiciуn. Es decir, el tiempo de vuelo es aquel para el cual la altura es 0 (se llega al suelo).

y=H+v0y⋅t−12⋅g⋅t2=H+v0⋅sin(α)⋅t−12⋅g⋅t2 (igualando esto a 0)

Por las dudas:

H = altura
v0y = velocidad inicial y
v0 = velocidad inicial
t2= tiempo al cuadrado
g = gravedad
vx = velocidad x
α = alfa
sin = seno
cos = coseno

En resumen, es un huevo, no sй como hacerlo en Pawn.

[OTACON]

y por que un off-topic si lo que necesitas es para pawn. -.-

[Swedky]

Quote:

Originally Posted by JeffreyG Por lo que leн tenes que saber el tiempo de vuelo, y sustituirlo en esta ecuaciуn, esto te va a dar el alcance, osea la distancia que recorrerб el objeto: x=vx⋅t=v0⋅cos(α)⋅t El tiempo de vuelo se calcula igualando a 0 la componente vertical de la posiciуn. Es decir, el tiempo de vuelo es aquel para el cual la altura es 0 (se llega al suelo). y=H+v0y⋅t−12⋅g⋅t2=H+v0⋅sin(α)⋅t−12⋅g⋅t2 (igualando esto a 0) Por las dudas: H = altura v0y = velocidad inicial y v0 = velocidad inicial t2= tiempo al cuadrado g = gravedad vx = velocidad x α = alfa sin = seno cos = coseno En resumen, es un huevo, no sй como hacerlo en Pawn.

Sн pero por ejemplo la inclinaciуn inicial es de 90° la distancia serб 0 independientemente del tiempo y la velocidad inicial

Quote:

Originally Posted by OTACON y por que un off-topic si lo que necesitas es para pawn. -.-

Bбsicamente lo que preguntй no tiene nada que ver con PAWN...

[OTACON]

Quote:

Originally Posted by EnzoMetlc Sн pero por ejemplo la inclinaciуn inicial es de 90° la distancia serб 0 independientemente del tiempo y la velocidad inicial Bбsicamente lo que preguntй no tiene nada que ver con PAWN...

si tu quieres obtener la formula de hacer algo y que te lo pasen a pawn... teуricamente, tiene que ver con pawn.

saludos.

[JeffreyG]

Quote:

Originally Posted by EnzoMetlc Sн pero por ejemplo la inclinaciуn inicial es de 90° la distancia serб 0 independientemente del tiempo y la velocidad inicial

Si la inclinaciуn es de 90є usa sуlo la ecuaciуn de movimiento en el eje y.

La v0y es = a H

[marconol]

La fуrmula de la distancia horizontal recorrida estб en el comando .

Код HTML:

CMD:calcular(playerid, params[])
{
	if(IsPlayerConnected(playerid))
	{
		new str[57], Float: Distancia;
		new Float: Velocidad_Inicial = 10.0;//en m/s
		new Float: Gravedad = 9.81;//m/s2
		new Float: Angulo_De_Inclinacion = 80.0;//grados
		//Seno y Coseno necesario para aplicar en la fуrmula
		new Float: Seno_De_Angunlo = floatsin(Angulo_De_Inclinacion, degrees);
		new Float: Coseno_De_Angunlo = floatcos(Angulo_De_Inclinacion, degrees);
		//Fуrmula
		Distancia = 2 * floatmul(Velocidad_Inicial, Velocidad_Inicial) * floatmul(Seno_De_Angunlo, Coseno_De_Angunlo) / Gravedad;
		//Mensaje del resultado
		format(str, sizeof(str), "La distancia horizontal recorrida es: %0.2f metros.", Distancia);
		SendClientMessage(playerid, -1, str);
	}
	return 1;
}

[MaRcOsWeB]

Tienes varios errores conceptuales, la velocidad se mide en m/s, no en m/s^2, dado que si tomas en cuenta eso, estamos hablando de la aceleraciуn, que es la derivada de la velocidad (dv/dt).

Si estamos hablando de un movimiento parabуlico, tu bбsicamente quieres saber el alcance mбximo que tendrб un cuerpo a una determina velocidad. Eso se calcula de la siguiente manera:

Para empezar, tenemos que tener en cuenta que el movimiento parabуlico es un movimiento bidimensional (dos dimensiones), es decir, un cierto movimiento en x, y cierto movimiento en y. La funciуn que expresa el tiro parabуlico es una parбbola (vaya deducciуn), por lo cual, tendremos dos raнces en el eje de abcisas (eje x), que determinarбn a donde cayу el proyectil. Espera... їCуmo quй dos? Bueno, si, teoricamente habrб dos, pero fisicamente solo habrб una.

їEntonces?
Para obtener las raнces de una parбbola, se iguala la funciуn a 0, es decir, y = 0. (Siendo y = f(x))



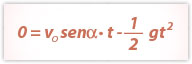
їY quй son todos esos valores? Bien, te respondo:
v0 es la velocidad inicial del proyectнl.
α es el бngulo con que se dispara el proyectнl.
t es igual al tiempo.
g es la gravedad.

їPero no puedo lograr una ecuaciуn independiente del tiempo? ЎClaro que si!

Si haces un par de reemplazos y artilugios matemбticos, obtienes el alcance mбximo con respecto a una cierta velocidad y бngulo establecidos.



їY quй es sin (2α)? Es igual a 2.sin(α).cos(α)

Una ъltima cosa, їy el tiempo de vuelo? ЎFбcil!



Entonces ya tienes, alcance mбximo y tiempo de vuelo con respecto a ciertos valores. Recuerda tener en cuenta que este caso es para cuando tanto el blanco como el lugar de disparo estan a la misma altura.

Espero que te haya servido.

ЎSaludos!

Edit: Te dejo ademбs un informe sobre parбbola de seguridad que hice para la universidad, te vendrб de utilidad.
Link al documento: https://*******/oB24aW